According to the final results, it seems that this task was the most difficult, but, as we will see in a moment, it wasn't really so bad.
First, let's have a look at the easy data set, b1. After a short examination one can figure out that all bacteria (ok, let's call them simply points) are on a single line. What does this mean? Well, something more than they are on a line. It also means that a simple binary-search can be performed to find out the color boundary.
According to the statement of the problem, we may assume that there are at least 30% red points as well as 30% green points. Because the points are on a line, these 2*30% points must be at the ends of the line, one color at one end, the second on the other end. So, instead of 7474 points, we have just about 2990 points of unknown color (plus we don't know which end of line is red and which one is green).
For the simplicity of the following, as the points are on the line, we can re-order them according to their position on the line; then, we can address point at one end as 0, the point at the other end as 1, and the point that is in the middle as 0.5, etc.
Let's start the binary-search. In the first submit, we will ask for the points 0.3, 0.5 and 0.7. We already know that exactly one of the points 0.3 and 0.7 is red and exactly one is green. This gives us information about which end of line is red and which one is green. Furthermore, according to the color of point 0.5, we can say that either points 0-0.5 have color of point 0.3, or points 0.5-1 have color of point 0.7, so just now we don't know the color of just 20% of all points, that is about 1500 (it can be interval 0.3-0.5 or 0.5-0.7).
The following submits are simpler - without any care, divide the interval of unknown color by 3 points into 4 equal parts, ask for the color of these 3 points, and we get an interval of quarter length. So, after 2nd submit we have at most 375 points of unknown color, after 3rd submit we have just 94 points left, after 4th... Stop! What is the error we can afford? Right, it is 2% of 7474 that is 149. So, in the 4th submit guess any line, which divides our interval of unknown color, and it's done!
And now the main point of this problem, the difficult data set b2. We have many points in the square with opposite corners at (0,0) and (1,1). At the beginning, we don't know the color of any point. What to do now?
Let's examine this problem a bit. If we have 3 points of equal color, we know that all points inside the triangle determined by these 3 points have the same color; if not, we wouldn't be able to divide points by a straight line.
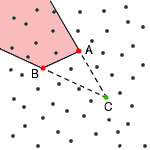Another important case is when we have 2 points (named A,
B) of one color, let's say red, and one point (named C) of
another color, in this case green. Now, all points that are
behind the segment AB, when looking from C, must
have the color of A (or B, if you want), otherwise the
division by a straight line wouldn't be possible. In the picture, all
points in the red area should have red color.
So, we will have 3 sets of points:
At the beginning, set Uncolored contains all points and sets Red and Green are empty. When we ask for the color of some point, we move that point into set Red or Green, depending on its color. Now, we can perform the coloring:
We can speed up this algorithm by choosing points only from convex hulls of points from sets Red and Green.
After we have colored as many points as we can, we have to make a guess for the dividing-line and for another 3 points (preferably from set Uncolored, since we know colors of the rest). We can solve this task in two different ways - let the computer do it, or let it on the user. Surely, user can better select points that might be helpful for our coloring. As our solution shows, it also suffices to take 3 random points from set Uncolored; this surely is not optimal, but requires no user action and gives relatively good results.
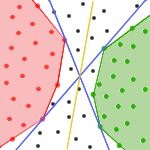Our solution also makes a guess for dividing-line, as follows. The
set Uncolored can be divided by many lines, but there are two of
our interest. These 2 lines are the outermost ones in sense of slope -
all other lines have slopes between the slopes of these two (blue lines
in the picture). We choose always the line that is in the middle of
these two (yellow line in the picture), assuming that this might be
quite close to the real dividing-line (actually, it can be any of all
possible lines; unfortunately, we can't say which one, so we just
choose).
The described algorithm solves this problem in most cases with 6-8 tries, depending mostly on the selection of points to ask for; the worst case observed was 11 tries (in which case several points we asked for were nearly useless; random choice is not always the best choice).
Finally, there is still one thing to mention. As probably many of you found out, there is someone's face encoded in the data set b2:
But, who's that? Is it someone from IPSC organizing team? No... Well, have a look...:-))
