The forest is represented by a 0,1-matrix. We will call the values 0 and 1 colors, 0 being white and 1 black. Instead of selecting a tree that has to be enchanted we select the corresponding element of our matrix. It is simple to divide the matrix into maximal connected one-colored areas. The spell performs a flood-fill starting at the selected element – the whole area containing the selected element changes color (from white to black or vice versa).
Let's construct a graph Gm = (V,E) where vertices will represent the areas in the matrix. Two vertices will be connected by an edge iff the corresponding two areas are adjacent (e.g. one of them contains an element with the coordinates (a,b) and the other an element (c,d) such that |a-c|+|b-d|=1). With each vertex we store its color. Note that all neighbors of a white vertex are black and vice versa.
What will happen with our graph after casting the spell? The selected area will change its color and merge with all neighboring areas into one larger area. Or, speaking in graph terms, we join the selected vertex and all its neighbors into one "large" vertex. Its color will be the opposite of the color of the selected vertex. We may throw away all the loops (previously edges between the selected vertex and its neighbors). We will call this operation a contraction of the vertex v. Note that also after any contractions all neighbors of a white vertex are black and vice versa. Our goal is to create a graph with only one vertex using as few contractions as possible.
Let G be an undirected graph. We start by defining some terms:
Lemma 1: After a contraction of a central point c the radius r of the graph decreases (at least by 1).
Proof: For each neighbor v of c we have d(v,c) = 1. Consider a vertex u != c, take any shortest u-c path. It leads through exactly one neighbor v of c. Therefore d(u,c) = d(u,v) + d(v,c) = d(u,v) + 1. It follows that the eccentricity of c' after the contraction will be one smaller than the eccentricity of c before the contraction. Let r' be the radius of the contracted graph. We know that r'<=ex(c') and ex(c')<ex(c)=r, q.e.d.
Lemma 2: Let c be any central point. After a contraction of any vertex v in V the eccentricity of c stays the same or decreases by 1.
Proof: Suppose v=c. We already proved that after a contraction of c its eccentricity decreases by one. Now suppose v!=c. Proof by contradiction. Clearly the eccentricity of c may not increase, therefore suppose it decreases at least by two. For each vertex u we take an arbitrary shortest c-u path Pu. As c is a central point, the length of some Pu is r. We will now find a vertex b such that ex(b) was less than r before the contraction. This will be a contradiction, because the eccentricity of c was the smallest one.
We assumed that after the contraction ex(c)<=r-2. Consider the paths Pu. Some of them were already shorter than r-1 before the contraction, we won't be interested in these. At least one of them had length r. Each Pu of length r is now shorter at least by two. It follows that either this Pu passes through v or through at least three neighbors of v. Without loss of generality (why?) we may assume the first case. Each Pu of length r-1 is now shorter at least by one. It follows that either this Pu passes through v or through at least two its neighbors.
Let b be the first vertex on some shortest c-v path (a neighbor of c). We will show that (in the graph before the contraction) ex(b)<r. Let u be an arbitrary vertex. We consider the following cases:
- Case 1. d(c,u)<=r-2.
Then d(b,u)<=d(b,c)+d(c,u)=1+(r-2)=r-1.- Case 2. d(c,u)=r-1 and Pu passes through two neighbors v1,v2.
We may assume that d(v1,v2)=1, otherwise there is a shortest c-u path passing through v, we will handle this vertex in case 3. We know that the shortest b-u path is not longer than the shortest b-v-v2-u path. We also know that d(c,v)<=d(c,v1)+1, therefore d(c,v)-1<=d(c,v1).
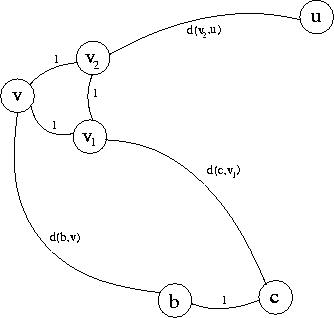
We have: d(b,u) <= d(b,v)+d(v,v2)+d(v2,u) = (d(c,v)-1)+1+d(v2,u) <= d(c,v1)+d(v1,v2)+d(v2,u) = d(c,u) = r-1. Or the same in words: there is a b-u path (leading through v and v2) that is at most as long as the shortest c-u path (leading through v1 and v2). The following image may help if you have problems understanding this step of our proof.
- Case 3. r-1<=d(c,u)<=r and Pu passes through v.
We know that d(c,u)=d(c,v)+d(v,u). But d(b,v)=d(c,v)-1 and thus d(b,u)<=d(b,v)+d(v,u)=d(c,u)-1<=r-1.We have reached a contradiction – ex(b)<r but then c is not a central point. Therefore our assumption was wrong and the lemma is proved.
Theorem: The least number of contractions needed to contract the whole graph into a single vertex is r.
Proof: Follows from the above lemmas. Let c be any central point. After arbitrary r-1 contractions ex(c)>0 and therefore the graph has at least two vertices. On the other hand r contractions suffice – e.g. always contract the vertex c.
The algorithm is now pretty straightforward – we have to transform the given matrix to a graph and find its central point. The transformation can be easily done in O(RC) time. Then we will compute the eccentricity of each vertex by running a BFS (breadth first search) from each vertex. The time complexity of this part is O(N(M+N)), where N is the number of vertices and M is the number of edges of the graph. Note that the graph is planar, therefore M=O(N). The resulting time complexity is therefore O(RC+N2). (In the worst case this is O(R2C2).)