Let us represent the unconnected contacts as nodes of a graph and pairs of compatible contacts will be edges. Now, the problem is to count the number of perfect matchings. In general this problem is very hard. To solve it, we must exploit special properties of graphs given in the inputs.
Otherwise absolutely useless coordinates in the input file were useful for drawing the graphs so that it is easy to see their special properties. See the drawings: easy.ps and hard.ps or hard.png. The drawings were created by this short utility.
We can see that all graphs in the easy input file are composed of rather small connected components. In each component, the number of perfect matchings may be determined by exhaustive search that tries all possible matchings. The number of perfect matchings of a graph is the product of numbers of perfect matchings of all its connected components.
In the hard input, there is a graph with four different kinds of connected components:
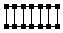Number of
perfect matchings in such graph with 2n nodes is
F(n), where F(1) = 1, F(2) = 2, and F(i+2) =
F(i) + F(i+1) for i > 0.
Number of perfect matchings in such graph
with 6*n nodes is G(n), where G(1) = 3,
G(2) = 11, and G(n+2) = 4*G(n+1) - G(n) for i > 0.
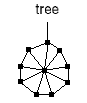with n nodes. If n is even this graph has n-1
perfect matchings, if n is odd there is one node in the graph
that is always (in every perfect matching) matched to the same node
in the tree. Number of perfect matchings of the rest of this graph is
(n-1)/2. In every perfect matching each of leafs of the tree
that are connected to some graph will be connected to the same
node. Either to one in the tree (if the connected graph has even
number of nodes) or to one in the connected graph (if it has odd
number of nodes). As long as the tree has at most one perfect
matching, the number of perfect matchings of the whole connected
component is either the product of numbers of perfect matchings of
all the graphs connected to tree leafs or zero, depending on whether
the rest of the tree is matchable. The total number of perfect matchings of the graph is again the product of numbers of perfect matchings of all connected components.
