Internet Problem Solving Contest

• Easy input data set – G1
• Hard input data set – G2

Peter works in the Slovak Institute of Gears. After years of hard work he has constructed a special machine. Its only purpose is to rotate a lot of gears. After he was watching it for three hours (it makes a good mechanical "screensaver"), he got interested in one mathematical problem.

In the machine there are N gears next to each other. (This means that for each i the wheel i is connected to the wheels i-1 and i+1 – except for wheels 1 and N that have only one neighbor each.) The hidden engine rotates the first gear clockwise one tooth per second. As the gears are connected, all other wheels rotate at the same speed, too. The i-th gear has a_i teeth numbered counter-clockwise from 0 to a_i − 1. There is also one red mark next to each gear. At the beginning the wheels are rotated so that the 0th tooth of each wheel is next to its mark.

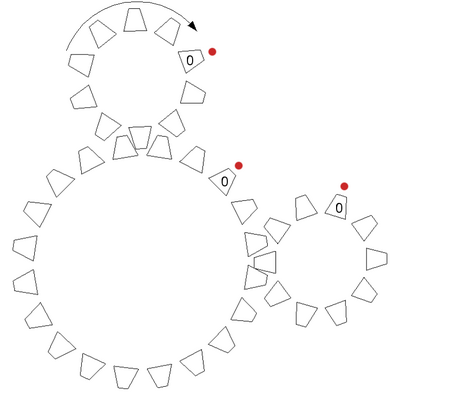
Peter has imagined a configuration of wheels. In his configuration for all i the i-th wheel has the tooth b_i next to its red mark. He would like to know whether his machine will reach this configuration – and if yes, when it will happen for the first time.

Input specification

The first line of the input contains one integer M – the number of test cases. For each test case there is one integer N denoting the number of gears. N lines follow, one for each gear. On the i-th of these lines there are the numbers a_i and b_i described above.

Output specification

For each test case output one line with the first time when the i-th gear will have the tooth number b_i next to the red mark (for all i at the same time). If this never happens, output one line with the string "Impossible" (without the quotes) instead.

Example

Input:

2
3
5 2
4 2
6 4 
2
4 3
6 0

Output:

22
Impossible

---

Credits:
Problemsetter(s): Lukas
Contest-related materials: Lukas, Mirko