This problem was an instance of Post correspondence problem. You have to find such sequence a[1], a[2], ..., a[n], that strings xa[1]xa[2]...xa[n] and ya[1]ya[2]...ya[n] are equal. There doesn't exist an algorithm for this problem in general.
Let the sequence from the problem statement be x1,x2,...,x334 and let the sequence from the wrong program be y1,y2,...,y334. Our first observation is that a[1] must be 333, because we can't begin with nothing else. Also a[n] has to be 334. For i less than 333 it is true that the size of xi is equal yi (in fact, the size of strings x333 and y334 is 1 and the size of all other strings is 16). So after we add xi, yi, i<333 to both strings, the difference of their lengths won't change.
Our algorithm will be a breadth-first-search where vertices of graph will be strings. Let the vertex be a string r. That means xa[1]...xa[i]=ya[1]...ya[i]r for some a[1], ..., a[i]. When we add a[i+1] to the sequence, we get new string g: xa[1]...xa[i]xa[i+1] = ya[1]...ya[i]ya[i+1]g. Our goal is to find the shortest sequence a[1], ..., a[n] such that the corresponding string is empty − xa[1]...xa[i] = ya[1]... ya[n] and the sequence a[1],...,a[n] is the right input for both programs.
All the strings we get during the breadth-first-search will be of length 15 or zero. We have to start with x333 and y333. The difference of their lengths is 16− 1=15. We can continue with xi, yi, i< 333, their difference of lengths is 0. We can also continue with string x334 and y334, their difference of lengths is −15. We can't add number 333 to the sequence when the difference of lengths is 15, because there will be string "22" in the sequence and there will be no "22" in the corresponding part of xa[1]...xa[i]. So no string during the breadth-first-search will be of size 30 and more.
Our breadth-first-search will find the shortest way to empty string. We only have to reconstruct the sequence a[1], ..., a[n] and output it.
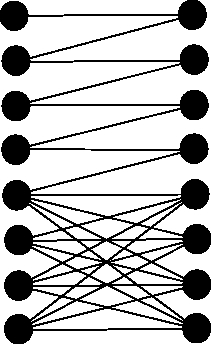
We have to find out, what does the program do. First it checks whether the input has 50≤ N ≤ 100. Then it transforms the original bipartite graph into normal graph and checkes whether the graph has at least N2+2N edges.
If all these tests succeed, it runs a modified Depth-first-search. If you take a better look at it you can recognize code for finding bridges in a graph. The number of bridges in the graph is stored in variable cnt. If the number of bridges is at least 2N, the programs outputs it.
So we have to find a bipartite graph with at least N2+2N edges and at least 2N bridges. The maximum matching can't be more than 2N, so the number of bridges has to be exactly 2N. Here is a solution for N=4 (the idea can be used for larger N):