In case you are not familiar with the Sudoku puzzle, please refer to the last section of this problem statement before reading any further.
We would like to present our variation: the Cross-linked Sudoku.
In Cross-linked Sudoku you are given several Sudoku puzzles at once. In addition, some of the squares in some of the puzzles are colored. Your task is to solve the entire set of puzzles with the following additional restriction: Squares sharing the same color must contain the same number.
The restriction remains in place even if the squares are on different boards. The colors are independent, squares with different colors may contain the same number.
Given a Cross-linked Sudoku puzzle, find its solution. You may assume that the solution is unique.
The input file is an image file containing the puzzle. Note that the Sudoku boards in the input file are labeled by capital letters.
After solving the puzzle, order the boards by their letters. For each board, write the 9×9 numbers it contains in row major order. Separate the numbers by some whitespaces.
Input:
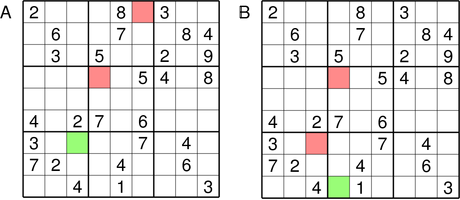
Output:
2 4 5 9 8 1 3 7 6 1 6 9 2 7 3 5 8 4 8 3 7 5 6 4 2 1 9 9 7 6 1 2 5 4 3 8 5 1 3 4 9 8 6 2 7 4 8 2 7 3 6 9 5 1 3 9 8 6 5 7 1 4 2 7 2 1 3 4 9 8 6 5 6 5 4 8 1 2 7 9 3 2 4 5 9 8 1 3 7 6 1 6 9 2 7 3 5 8 4 8 3 7 5 6 4 2 1 9 9 7 6 1 2 5 4 3 8 5 1 3 4 9 8 6 2 7 4 8 2 7 3 6 9 5 1 3 9 1 6 5 7 8 4 2 7 2 8 3 4 9 1 6 5 6 5 4 8 1 2 7 9 3
The solution for the example above is unique. Note that without the colored squares each of the separate puzzles would have more than one possible solution.
In a classic Sudoku puzzle, you are given a 9×9 grid that is partially filled with numbers 1 to 9:
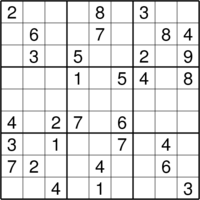
Your task is to fill in the remaining squares in such a way that in the end:
For the puzzle above, the only valid solution is:

Credits:
Problemsetter(s): Misof
Contest-related materials: Misof, Yulka