For cakes up to 3×3 we can try all possible combinations of cutting/not cutting of each edge between two neigbouring unit squares. For each such combination we can verify its validity as follows. We first compute the connected components of the cake (using the depth first search, or the breadth first search). Then we verify that there is no cut between two unit squares which belong to the same connected component.
For cakes of the dimensions 1×N (resp. N×1) all possible combinations are valid. This gives simple formula, 2(N-1), for the number possible cuttings.
For cakes of the dimensions 2×N (resp. N×2) we set up a recurrence as follows. Let us think of a 2×N cake as two rows of unit squares of length N each. We denote by aN the number of possible cuttings of a 2×N cake in such way that the two rightmost unit squares belong to the same connected component. Similarly, we denote by bN the number of possible cuttings of a 2×N cake in such way that the two rightmost unit squares belong to two different connected components. We readily check that a1 = 1 and b1 = 1.
The following picture demonstrates that aN=2aN-1 + 3bN-1:
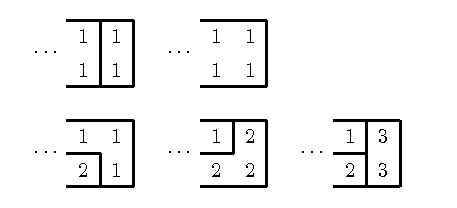
The following picture demonstrates that bN=3aN-1 + 4bN-1:
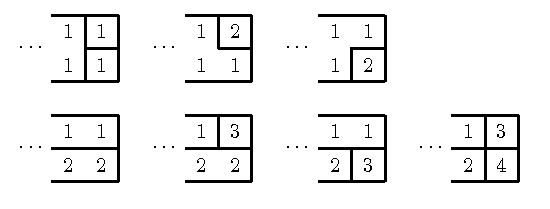
From these recurrences we obtain a2=5 and b2=7.
If we denote by sN the sum of aN and bN,
putting the two recurrences together gives:
sN =
(aN + bN) = 6(aN-1 + bN-1) + bN-1 - aN-1
= 6sN-1 + 3aN-2 + 4bN-2 - 2aN-2 - 3bN-2
= 6sN-1 + aN-2 + bN-2
= 6sN-1 + sN-2
and s1 = 2 and s1 = 12. This recurrence can be implemented in
a language which supports long integer arithmetic; the unix tool bc is ideal for such job.
(See bc script solving inputs 2×N.).
The solution for arbitrary dimension M×N is a generalization of the 2×N case, that is, we set up system of (linear) recurrences. However, our solution will work only for small values of M. In practice today's PC is able to handle M ≤ 5.
(An alternate view of the same situation: we will consider one dimension M to be fixed and use dynamic programming to compute the number of cuttings for each N.)
In our solution, for every partition p of the last (i.e. N-th) column into connected components, and every combination q which determines whether any pair of the components occuring in the last column touch each other somewhere in the cake, we compute the number a(N,p, q) – the number of different cuttings of the M×N cake obeying p and q.
This is best demonstrated on an example. We consider M=3 and the partition p=(1,2,3) of the last column:
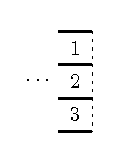
The partition p implies that components 1,2 touch and likewise 2,3. Moreover, let us assume that the components 1,3 do not touch anywhere in the cake before the last column. This is formally captured by the combination q={{1,2}, {2,3}}. (Formally q is a set of unordered pairs). Suppose that we have computed the value a(N-1,p,q).
We try all the possible valid combinations how to cut the last column. Several of them are shown are shown of the following picture.
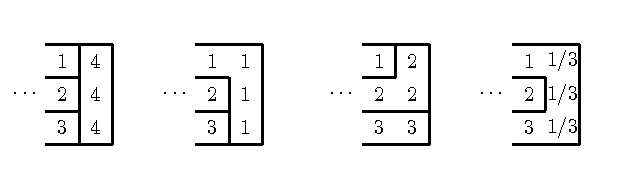
Note that the last combination is valid, since we assume that the components 1,3 do not touch anywhere before the last column.
Each of the valid combinations contributes a(N-1,p,q) to some a(N,p',q') for some p', q'. For example the first two combinations in the picture together with the last one contribute 3a(N-1,p,q) to a(N, p', q') where p'=(1,1,1) and q'={}. (Note that the partitions (4,4,4) and (1,1,1) and (1/3,1/3,1/3) are equivalent.) Likewise, the third option in the picture contributes 1a(N-1,p,q) to a(N, p'', q''), where p''=(2,2,3) and q={{2,3}}. (Or equivalently, p''=(1,1,2) and q''=(1,1,2).)
Thus, by trying all combinations of p,q and all ways how to cut the last, yields the coefficients of the linear system of recurrences for the numbers a(N,p,q). Using these coefficients we can compute the values a(N,p,q) for any N. For example for M=3, there are 4 options for p; ((1,1,1), (1,1,2), (1,2,2), (1,2,3)), and 8 options for q; ({}, {{1,2}}, {{2,3}}, {{1,3}}, {{1,2}, {2,3}}, {{1,2}, {1,3}}, {{1,3}, {2,3}} and , {{1,2}, {2,3}, {1,3}}). Thus the whole system of recurrences consists of 4*8=32 variables a(N,p,q) (for each N).
We omit couple of details, such as how to compute the initial values a(1,p,q), and how determine whether a particular cutting of the last column is valid for some p,q, and how to represent partions p and sets q.