The simplest way of solving this task was to make the following N questions: (1, 0, 0 , 0, ..., 0), (0, 1, 0, ..., 0), ..., and (0, 0, ..., 0, 1). Each of these questions gives us one number of the sequence. In the (N+1)-st submit Jan's correct sequence can be guessed. Sadly, for the hard problem N>9, so this solution can not be used. And even for the easy problem there is a much easier solution.
A more tricky approach can be taken by using the sequence: (1, 10D, 102D, 103D, ... , 10(N-1)D). For sequences (X1, ..., XN) and (1,10D, 102D, 103D, ... , 10(N-1)D) the scalar product is:
(X1, ..., XN) · (1,10D, 102D, 103D, ... , 10(N-1)D) = X1+X2.10D+...+XN.10(N-1)D.
Note that when the numbers Xi have at most D digits, they can be directly read from the scalar product.
For the easy input the value (N-1)D is larger than G, thus we can not use this exact approach. However, the modification is pretty simple: use two questions, and in each ask about one half of the sequence. Thus we need two questions and then one guess. In the hard input it is not that easy.
The values of D and G in the hard input are selected in such a way that the method mentioned above is not applicable. For the hard input, we will now show the minimal number of questions that we need to make.
Consider the maximal number of digits we can get by asking one question. Obviously, for the hard input, the largest number that can be obtained from the scalar product operation has 106 digits. When we ask Jan Q questions our program can get U=10Q*106 possible combinations of digits at most. Therefore after Q questions we can distinguish between at most U cases. The number of all possible Jan's sequences is V=10N*D, in our case 1014*55. We need to be able to distinguish between all possibile Jan's sequences, and therefore Q must be large enough so that U>V. The first integer value of Q for which this is true is Q=8.
Let us show a solution which uses 8 questions for the hard input (N=14, D=55, G=49). We will use an approach based on a similar idea to the one mentioned above. Let us suppose that we ask a question (0, 0,..., 0, 1, 10G-1, 0...0) where the number 1 is in the 2i-th place of the sequence for some i (and the number 10G-1 is in the (2i+1)-st place of the sequence). The scalar product of Jan's sequence and this sequence will be called W. Then the number W has the last G-1=48 digits same as are last 48 digits of the 2i-th number in Jan's sequence, and the first G-1=48 digits almost equal to the first 48 digits of the (2i+1)-st number in Jan's sequence. (When talking about the first digits, we consider each of Jan's numbers to have exactly D digits, possibly with some leading zeroes. The word almost is due to the fact that a carry may happen at the boundary.)
For a better understanding see the following picture. In the picture, there is an addition of two numbers (A and B): A has the size of D=55 digits and B has the size of D=55 digits as well, but it is shifted by G-1=48 digits to the left. Then you can see that the "overlap" of these two numbers during the addition has the size of 7 digits. We will later show that we can reconstruct A and B if we know the result of this addition W, and the last 8 digits of B (marked in the picture as 1+7).
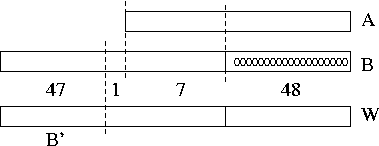
If we knew the last 8 digits of B, by comparing the most significant of them and the corresponding digit of W. If they are equal, or if the digit in W is one larger than the digit in B, the leftmost digits of W (marked B' in the image) are unaffected by the carry, and thus are equal to the leftmost digits of B. The remaining case is when the digit in B is 9 and in W 0. In this case the rest of W is affected by the carry, and thus B=B'-1.
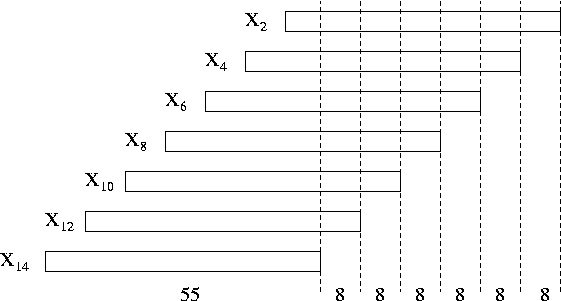
Our first seven questions will be (1, 10G-1, 0, ... 0), (0 , 0, 1, 10G-1, 0 ... 0), ..., and (0,0,...,0,1,10G-1). We now have seven times the situation we solved above. All we need to know are the last 8 digits of each of the numbers X2, X4, ..., and X14. Once we find out these digits we are done.
We can find out the missing digits using a single question: (0, 1, 0, 108, 0, 1016, ..., 0, 1048).
The last 8 digits of the answer Y we get are the last 8 digits of X2. Using these we compute X2 (and X1), and now subtract X2 from Y, and divide Y by 108. We will now use the same approach to restore X4, and so on. See the following picture for a visualisation of the process.