For images of sizes which fit into memory, say up to 1000×1000, we create an array and draw the whole image into it using the given algorithm. Afterward we execute floodfill using black color. There are several possibilieties how to implement the floodfill operation - either depth first search or breadth first search, or, to speed things up, using scanline fill. At the end, we simply count the pixels of individual colors.
However, the above algorithm does only work for easy input case (unless you have about 1TB of memory). Different approach exists - in computer graphics, filled complex polygons are usually drawn using the scanline algorithm. The basic idea is that when we pass from left to right along a horizontal line, we draw pixels at positions that have odd number of polygon segments crossing this horizontal line to the left.
Unofortunately, this algorithm would require some tweaks to do its job, since due to line rendering algorithm, parts of two line segments can touch each other, preventing the floodfill to reach them. You could end up with something like this:
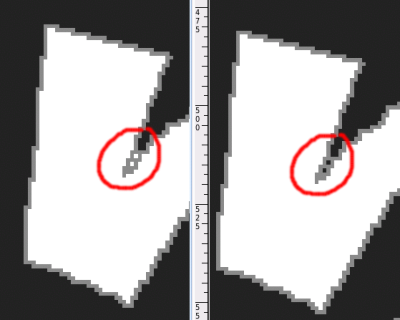
Note: as the problem statement didn't specify whether jPix's floodfill is 4-way or 8-way, we would accept both possibilities (last testcase in hard input file would fill 2 more pixels using 8-way floodfill).
The actual solution used is a modification of original floodfill idea, however working on a compressed bitmap instead of raw 2D array of pixels. We use RLE - Run-Length Encoding - which is rather simple to work with and in this scenario achieves great size reduction, although in some cases could be much worse then raw bitmap - imagine checker-board pattern. However we have the inputs available so we can check that such case will not happen.
We represent each line of the bitmap as a series of lengths of same-color pixels (let's call them chunks). We need 3 different colors, so we allocate 2 bits in an 32 bit int for color and rest for chunk length. This way, memory needed to store one line doesn't depend on actual image width, but rather on number of grey pixels (ie, polygon segments this line intersects). Clearly for 'normal' images this works pretty well.
Once we have this bitmap ready, we can just start floodfill operation, which will work the same way as scanline floodfill algorithm, without the need to fill all pixels in a row in a cycle since they are packed into one chunk. We need to detect which chunks of previous/next image row should also be filled - that is in fact a problem of finding overlapping intervals in two sets of intervals. When we have this, we can just start the floodfill from first image row (which is represented by a single chunk) either recursively or using a queue. When finished, we just sum up chunk lengths of white, grey and black pixels and we're done.
The only obstacle now is how to create the bitmap based on input specification. For each line specified in the input, we create a 'list' of grey pixels. We store this 'list' in a vector<set<int>>, where the vector holds all image rows, while the set contains a set of X-coordinates of all grey pixels in that row. From this representation it is then straightforward to create RLE-encoded bitmap.
This algorithm can solve hard input case in about a minute on common PC with 1GB of memory; the algorithm itself needs about 700MB of memory (out of which the RLE bitmap eats up just about 10%). We could easily reduce this by not creating the list of grey pixels at once, but splitting it into ie. 10 passes, each covering 1/10 of bitmap rows.