Let p(i,j) be the number of ways i people can sit in a row so that the last j positions are occupied by women and positions 1 and i-j are occupied by men. It’s clear that p(1,0) = 1,p(1,1) = 0 (we don’t allow a woman to sit at position one). For i > 1 we have p(i,0) = ∑ j=0k-1p(i- 1,j). In this possibility we add a man to the end of the row. For i > 1 and 0 < j ≤ k we have p(i,j) = p(i - 1,j - 1). Here we add a woman to the end of the row.
If assignment A can be made from assignment B by rotating all the people around the table, we call these assignments isomorphic. Let r(l) is the number of ways people can sit around the table of length l such that there are at most k women next to each other (position 1 is next to l). Now, we do not consider isomorphic assignments equal. Because we have calculated numbers p(i,j) for i ≤ n and j ≤ k, we can calculate values r(i) for 1 ≤ i ≤ n. The value p(i,j) denotes the number number of ways i people can sit in a row so that at positions i - j + 1,i - j + 2,…,i sit women and at positions 1 and i - j sit men. The first position is always occupied by a man. When we multiply p(i,j) by j + 1, we get the number of ways i people can sit around the table such that there is a group of j women starting at position between i - j + 1 and i inclusive. There can be at most k women next to each other, thus we get the formula
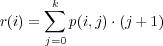
Let a1…al is an assignment of men and women around the table. We call this assignment
periodic if there exists an integer m∣l,m < l such that ai = ai mod m for every i. In other words
a1…al = 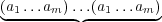 l∕m times. Let m is the smallest number such that ai = ai mod m for every i
and m divides l. It follows that the sequence a1…am is nonperiodic (we would have a contrary with the fact that
m is the smallest number) and assignment a1…al has m isomorphic forms. Let q(m) is the number
of nonperiodic assignments of length m, then q(m)
m is the number of nonisomorphic nonperiodic
assignments of length m. Let s(l) is the number of nonisomorphic assignments of length l. We get the
formula
l∕m times. Let m is the smallest number such that ai = ai mod m for every i
and m divides l. It follows that the sequence a1…am is nonperiodic (we would have a contrary with the fact that
m is the smallest number) and assignment a1…al has m isomorphic forms. Let q(m) is the number
of nonperiodic assignments of length m, then q(m)
m is the number of nonisomorphic nonperiodic
assignments of length m. Let s(l) is the number of nonisomorphic assignments of length l. We get the
formula
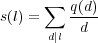
Now we know how to calculate the final result, but we don’t know how to calculate q(l). r(l) is the number of all assignment of length l, both periodic and nonperiodic. Hence we only have to substract from r(l) the number of periodic assignments:
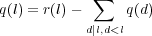
All our calculations are modulo prime number P = 100000007, hence we can do a division. The division by number a is done by multipling by aP-2, because aP-2 ⋅ a ≡ aP-1 ≡ 1 (mod P).
In the whole algorithm we ignored a possibility where there are only women around the table. We will handle this case separately. There is only one such assignment, therefore if n ≤ k we increase the result by one.
The slowest part of our algorithm is the calculation of numbers in the table p which can be done in time O(nk).