Internet Problem Solving Contest

• C++ program "not solving" the easy data set
• Python program "not solving" the hard data set

Strategy

There were two valid strategies. The simplest one was just to submit something clearly wrong as soon as you read the problem.

The second strategy, obviously, involves solving the problem to find the inputs that cause WRONG ANSWERs, and submit these for a time bonus.

For the second strategy, you have to make an educated guess whether to do it or not. More precisely, you should estimate how long it will take you to solve the task. Note that if you spend T minutes solving this task, then each of the tasks you solve afterwards will be submitted T minutes later, thereby accumulating your time penalty. Thus you should only attempt this strategy if you are fast.

Easy data set

Function foo is better known as Euclid’s algorithm calculating the greatest common divisor and function bar is a very clumsy way of testing primality of a given number: if p is a prime number then it doesn’t have a common divisor greater than one with any number q < p – gcd(p,q) = 1 for every 1 ≤ q < p. On the other hand, if n = d ⋅ k, than gcd(n,d) = d and gcd(n,k) = k, so the converse holds too.

Thus we get a WRONG answer only if we find a prime number n in the given interval 100000000–198765432 such that numbers n + 18, n + 36, etc. are also primes. These numbers couldn’t be found using the given program (in a reasonable time). It is way to slow even for testing a single number. A good way to solve this problem was to use the sieve of Eratosthenes and then sweep through the array and find the primes satisfying the given funny condition.

There are 14 such numbers: 186613711, 126605623, 143819771, 118810171, 123372071, 128293463, 196192091, 194990891, 172496083, 175066651, 132058483, 106961383, 117340703 and 142425763.

Hard data set

The hard problem was to find all the square roots of 1 (mod N). We call x a square root of a, if a is a square of x i.e., x² = a (equivalently, a square root of a is a root of the quadratic equation x² - a = 0).

The square roots may be different depending on what numbers we work with, for example:

• if we work with positive real numbers, there is only one square root of 3 (but there is no square root of 3 e.g. in rational numbers)
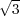• if we work with all real numbers, there are two square roots of 3 (both and - satisfy the definition above), but there is no square root of -1 (however, there are two square roots of -1 in complex numbers: i and -i)
• if we work with integers, there are two square roots of 4 (but no square root of 5 or -4)
• if we work with integers modulo 7, then 0² = 0, 1² = 1, 2² = 4, 3² = 9 ≡ 2, 4² = 16 ≡ 2, 5² = 25 ≡ 4 and 6² = 36 ≡ 1; so 1, 4 and 2 have exactly two square roots (mod 7) and 3, 5 and 6 don’t have a square root (mod 7);

In particular, note that there are two square roots of 1 – this is always true, if we work with integers modulo p, where p is any prime number (except 2). This is because x² - 1 = (x- 1)(x + 1) and this is 0 (mod p) if and only if p divides (x - 1)(x + 1), which is if and only if p divides x - 1 or p divides x + 1. If 0 < x < p, then either x = 1 or x = p- 1. Note that p- 1 is the same as -1 (mod p) and it is easy to see that (-1)² = (+1)² = 1 (mod p). To sum up:

• if we work with integers modulo n, where n is not prime, then 1 and n - 1 ≡ -1 (mod n) are surely square roots of 1, however, there are more; for example take integers modulo 15, then 1² = 1, 14² ≡ (-1)² = 1, but also 4² = 16 ≡ 1 and 11² = 121 ≡ 1 (mod 15) – note that actually 11 = -4 (mod 15), so we should have already known that 11² ≡ (-4)² = 4² ≡ 1.
• finally, lets take pairs of integers (a,b) modulo 7; lets multiply these pairs this way: (a,b) ⋅ (c,d) = (ac mod 7,bd mod 7), so in particular, (a,b)² = (a² mod 7,b² mod 7); what are the square roots of (1,1)? well, we already know that there are two square roots of 1 modulo 7, namely ±1 so there are exactly 4 square roots of (1,1), namely: (+1,+1), (+1,-1), (-1,+1) and (-1,-1)

The last example may be obviously generalized to a simple fact:

Now how can we find the square roots mod 15? A “low level” approach: 15 = 3 ⋅ 5, so if 15 divides x² - 1 = (x - 1)(x + 1), then either 15 divides (x - 1) (so x = 1), or 15 divides x + 1 (so x = 14), or 3 divides x - 1 and 5 divides x + 1 or 5 divides x - 1 and 3 divides x + 1. Take the last case: x - 1 = 5k and x + 1 = 3ℓ (for some k,ℓ), so x = 5k + 1 = 3ℓ - 1 and 3ℓ - 5k = 2. Numbers k and ℓ can be found using extended Euclidean algorithm (see http://en.wikipedia.org/wiki/Extended_Euclidean_algorithm, http://en.wikipedia.org/wiki/Bzout’s_identity).

A more “high level” view: There is a one-to-one correspondence between numbers mod 15 and pairs (a,b), where a is mod 3 and b is mod 5; specifically, number n corresponds to pair (n mod 3,n mod 5). Furthermore, multiplying two numbers mod 15 corresponds to multiplying the corresponding pairs; in particular, square roots of 1 mod 15 correspond to square roots of (1,1) mod 3,5. We already know the square roots of (1,1) are (+1,+1), (+1,-1), (-1,+1) and (-1,-1). Thus all square roots of 1 mod 15 are numbers x such that

Chinese remainder theorem: Given pairwise coprime integers n₁,…,n_k and any integers a₁,…,a_k, the system of simultaneous congruences

has one unique solution mod N = n₁ ⋅ n₂n_k.

To solve the hard problem you should factorize number N first.

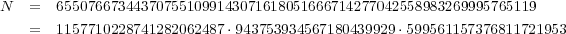
Since N = pqr is a product of 3 prime numbers, there are exactly 8 square roots mod N corresponding to tripples (±1 mod p,±1 mod q,±1 mod r). To find them we used the following program:

Excluding the trivial square root 1 (which gave correct answer), these 7 numbers gave the WRONG ANSWER:
655076673443707551099143071618051666714277042558983269995765118,
423708042681157396922466745853617748770106296874520998638487956,
409195345538471765371894681196161478839399343815134048305305493,
477249958667785939903924716186324105819048444428311493047736788,
231368630762550154176676325764433917944170745684462271357277163,
245881327905235785727248390421890187874877698743849221690459626,
177826714775921611195218355431727560895228598130671776948028331.
(The first number, N - 1 ≡-1 mod N, could be found without much effort.)