First of all, if the number of girls N is greater than the number of places K, the probability that some girl has no place to sit is clearly 1. In the rest of this solution we assume that N ≤ K.
We can turn the task into a combinatorial one. Instead of computing the probability, we can compute the number of bad sequences.
We can also use complementary counting. Instead of counting the bad sequences, we will find the number of good sequences – i.e., sequences such that all girls find a place to sit.
We will now present a simple argument that can be used to count the good sequences.
Imagine that the girls decided to practice this activity at home. However, instead of using K chairs in a row, they decided to use K + 1 chairs and placed them in a circle so that the numbers increased clockwise.
The rest of the game remains essentially the same as before – one after another, each girl enters the circle at the chair with the number she has on her ticket, walks clockwise until she finds the first free chair, and sits down.
As an example, consider the case K = N = 4. We have K + 1 = 5 chairs numbered 1 to 5. Each of the N = 4 girls generates a random number between 1 and 5, and then enters the circle and finds her place.
Suppose that the generated numbers are 5, 3, 3, 4, in this order. The first girl sits at the chair #5, the second one at #3. Then the third girl arrives. Her desired chair #3 is already taken, hence she sits at #4. Finally, the last girl arrives. Chairs #4 and #5 are taken, hence she sits at chair #1. In the end, chair #2 remained empty.
Remember that we assume N ≤ K. Hence whenever this modified game is played, each girl will find a place to sit, and some of the chairs (exactly K + 1 - N of them) will remain empty.
Each of the N girls has exactly K + 1 chair numbers to choose from, hence there are exactly (K + 1)N ways in which the game can be played.
Imagine that the girls played each of the (K + 1)N possible games once, and after each game they placed a coin on each of the K + 1 - N chairs that remained empty.
Now comes the most important observation: The game on the circle is perfectly symmetric. Hence after the girls played all (K + 1)N games, we must have the same number of coins on each of the chairs.
And as the girls placed C = (K + 1)N ⋅ (K + 1 -N) coins, the number of coins on each of the K + 1 chairs must be C∕(K + 1) = (K + 1)N-1 ⋅ (K + 1 - N).
We just proved the following fact: In the game on the circle, there are exactly (K + 1)N-1 ⋅ (K + 1 - N)
sequences of chair numbers such that the chair number K + 1 will remain free at the end. Let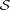 
be the set
containing these sequences.
Observe that no sequenc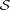e in may contain the number K + 1 – because if it did, the first girl with the
number K + 1 would sit there, hence chair K + 1 would not be free at the end. Thus each sequence in 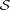only
contains numbers 1 to K.
And we are almost done. It’s now easy to see that the set 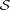are precisely all the good sequences in the
original game.
(If a sequence is good in the original game, this means that no girl “overflows” past the seat number K – hence if we play it on the circle with K + 1 chairs, chair K + 1 will remain empty. And vice versa.)
Hence in our original game, out of all A = KN sequences we have G = (K + 1)N-1 ⋅ (K + 1 -N) good ones. The answer is then 1 - G∕A.
(Note that the numbers K and K + 1 are always relatively prime, hence so are KN and (K + 1)N-1. Thus G∕A is always almost in reduced form, and the correct answer is easy to compute even if your programming language does not support big integers.)