The most straightforward approach was to perform an exhaustive search on all the possible seating arrangements. Although the time complexity of O((MN)K) is quite high, the memory requirements are quite favourable (O(MN)) and this approach is sufficient for the easy input set.
The hard case was a bit more tricky. All the test cases can be divided into three groups, each of them being solvable in a different way.
The first group consists of cases with M quite small (between 10 and 15) and N of modest size (up to 50). For this group, we can use the dynamic programming approach. It works by considering all the possible patterns of P occupied/free seats in each row and keeping track of the number AK,N,P of possible seating arrangements consisting of N rows, having K occupied seats and ending in pattern P (where P is a pattern of M bits). Then, calculating the value of AK,N+1,P is a matter of summing the corresponding AK′,N,P′ values for patterns P′ which could have been in the preceding row, which are compatible with pattern P (i.e. patterns which wouldn’t violate the no-adjacent-occupied-seats condition). Obviously, the number of seats we can use in the preceding N rows, K′, is equal to K minus the number of seats used in the latest, (N + 1)-th row. Implemented directly, this would yield time complexity of O(22MNK), as the number of possible patterns is 2M and we’re matching each of them against each.
This can be improved by realizing that if a pattern P′ is compatible with pattern P, then all sub-patterns of P′ are too (i.e. patterns created from P′ by leaving out one or more occupied seats). In fact, patterns compatible with P are precisely all the sub-patterns of the complement of P (which might not be an admissible pattern in itself, though). Thus, if we could calculate for each pattern the total number of seating arrangements it and its sub-patterns produce, and do so in an efficient way, we’d be done!
It turns out that this is possible – by considering the seats in the pattern one by one and adding the numbers of arrangements provided by the pattern without the seat occupied to the number of arrangements with that seat occupied. The total time complexity of this approach is then O(2MMNK), while it uses O(2MK) memory.
The second group consists of cases with very small M and very large N. Unfortunately, the N factor in the approach mentioned above prevents us from using it directly. However, if one looks at the dynamic programming and recalls that all the calculations performed were linear, it’s immediately obvious that the whole process can be seen as multiplication of a vector consisting of 2M.(K + 1) coordinates (the counts in the linear programming) by a huge square matrix of the same dimensions. Thus, in order to perform N steps, we only need to raise this matrix to the N-th power and that can be done in time proportional to log N rather than N. The price paid is both in the memory requirements which raise to O(22M ⋅ K2 and the cubic term in the resulting time complexity (2M ⋅ K)3.log N, originating from the matrix multiplication.
In fact, the base of the exponential could be lowered by considering only the admissible patterns, rather than
all of them – this would end up with the base being equal to the golden ratio ϕ = 
(
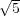+ 1), as the number of
admissible patterns of M seats is equal to the (M + 2)-th Fibonacci number and those grow exponentially, with
base ϕ.
Finally, the last group contains cases in which both M and N are quite large, which might look
scary…However, the value of K is always equal to either 1 or 2 – thus, allowing us to determine the answer
explicitly (in fact, it’s possible to give the answer in explicit way for each fixed value of K). For K = 1, the
answer is obviously MN (modulo the magic prime 420,047, of course). For K = 2, it can be easily seen
to be equal to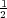 
((MN)2 - 5(MN) + 2(M + N)) by considering the placement of the first seat
(corners, sides or inside the rectangle) and the number of remaining possibilities for the second
seat.