Internet Problem Solving Contest

• Easy input data set – M1
• Hard input data set – M2

As Obi-Wan would put it: “This isn’t the problem statement you are looking for. Move along.”

The double factorial numbers are the numbers d_i defined by the following recursive formula: d₀ = 1, and ∀i > 0 : d_i = d_i−1 ⋅ i!. For example, d₃ = 1! ⋅ 2! ⋅ 3! = 12.

Sequences of length n with all elements belonging into the set {0,….n − 1} are called limited sequences of order n. For example, (0,2,0,1) is a limited sequence of order 4. The set of all limited sequences of order n will be denoted 𝒮_n.

The spread factor of a sequence A = (a ₀,…,a_n−1) is the value σ(A) = ∏ _i=0ⁿ⁻¹ ∏ _j=i+1ⁿ⁻¹(a_i − a_j).

There is a direct isomorphism between pairs of sequences and sequences of pairs. Formally: Let A,B ∈𝒮_n. We can denote their elements as follows: A = (a₀,…,a_n−1), B = (b₀,…,b_n−1). The corresponding sequence of pairs (a₀,b₀),…,(a_n−1,b_n−1)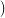 will be denoted P_A,B.

Pairs of integers can be ordered lexicographically in the usual fashion: (a,b) ≤ (c,d) if either a < c, or (a = c∧b ≤ d). A sequence P = (p₀,…,p_n−1) of pairs of integers is ordered lexicographically if for all i, p_i ≤ p_i+1. Let ρ(P) = [if P is ordered lexicographically then 1 else 0].

Let M be a n × n matrix, with rows and columns indexed from 0 to n − 1. Elements of M will be denoted m_r,c. A matrix is called a ℤ-var matrix if each element in the matrix is either an integer or a variable. The n-step traversal weight of M is the following value:

Problem specification

Given is a multivariate polynomial p with integer coefficients. Produce any reasonably small ℤ-var matrix M such that φ(M) = p.

Input specification

The first line of the input file contains an integer t specifying the number of test cases. Each test case is preceded by a blank line.

Each test case consists of a single line describing the polynomial. The variables are the letters a through z, the syntax will be clear from the input file. Each polynomial in the input file contains less than 50 operations (i.e., additions, subtractions and multiplications).

Output specification

For each test case output one matrix in the following format: First its size n, then all its elements in row major order. The elements may be separated by any positive amounts of whitespace. The size of the matrix must not exceed 70. All integers must be between −10⁹ and 10⁹, inclusive.

If for a given polynomial no such matrix exists, output a single zero instead.

Example