Internet Problem Solving Contest

• Easy input data set – Q1
• Hard input data set – Q2

Your physics lab report is due tomorrow. However, you had no time to do the required experiments, as you spent all your time practicing for the IPSC. Therefore you decided to write a fake report quickly. Here is how to get a good grade for your lab report:

• It has to contain a lot of measurements.
• You already know the correct value you were supposed to measure. The mean of all “measured” values in your report has to be equal to that value.
• The values must look sufficiently random to avoid suspicion that you made them all up. (Yeah, right.) More formally, they must have a sufficient variance.

Problem specification

You are given two integers: the desired mean μ and the desired variance v.

Pick a number of measurements n and the values of those measurements a₁,…,a_n such that the mean of those values is exactly μ and their variance is (easy subproblem: at least v / hard subproblem: exactly v). Formally, your values must satisfy the following conditions:

• 10 ≤ n ≤ 1000
• Each a_i is an integer between −10⁹ and 10⁹, inclusive.
• The value μ is exactly the mean: μ = (a₁ + ⋯ + a_n)∕n.
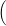• The variance of your values is computed as follows: (1∕n) ⋅(a₁ − μ)² + ⋯ + (a_n − μ)².

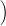  (If you are a statistics buff, note that we are not using the unbiased sample variance formula (the one with 1∕(n−1) instead of 1∕n), as in our case the mean is known a priori. If the previous sentence makes no sense, just ignore it and use the formula in the problem statement.)

• In the easy subproblem Q1: the variance of your values must be at least v.
• In the hard subproblem Q2: the variance of your values must be exactly v.

Input specification

The first line of the input file contains an integer t specifying the number of test cases. Each test case is preceded by a blank line.

Each test case contains a single line with two integers: μ and v.

You may assume that t ≤ 100, |μ|≤ 10⁶, and 0 ≤ v ≤ 10⁹.

Output specification

For each test case, output two lines. The first line should contain the number of values n, the second line a space-separated list of values a₁,…,a_n. Any valid solution will be accepted.

Example