Internet Problem Solving Contest

• Easy input data set – E1
• Hard input data set – E2

After the success of “open sesame!”, Ali Baba experimented with various other crops. Most of them didn’t do anything out of the ordinary, until suddenly “open sugarcane!” caused one of the rocks to shift and reveal the entrance to a peculiar cave.

The cave consisted of several chambers. The entrance lead directly into one of these chambers, we will call it the starting chamber. Some pairs of chambers were connected by one-way tunnels. Each of the tunnels was of one of three types: some tunnels had abrasive walls, others had battered walls, and the rest had calcified walls. As you have probably already guessed, we will denote the tunnel types a, b, and c.

For any chamber, there could have been arbitrarily many tunnels entering it, and arbitrarily many tunnels leaving it – including multiple tunnels of the same type, or no tunnels at all. Also, there could have been tunnels that start and end in the same chamber.

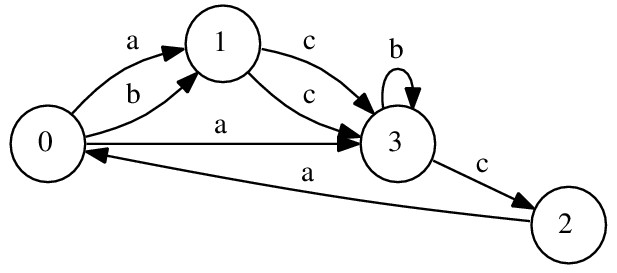
Of course, it’s not really a good idea to explore a cave with one-way tunnels on your own. Luckily, Ali Baba can enlist the help of the forty thieves (and their infinitely many friends, if necessary). One round of cave exploration looks as follows:

1. Ali Baba chooses a finite (possibly empty) sequence of tunnel types (a string of letters).
2. One after another, the thieves repeat the following procedure:
   1. The thief takes a long piece of rope and fastens one of its ends to his waist.
   2. He enters the starting chamber.
   3. He tries to follow a sequence of tunnels that 1. corresponds exactly to the sequence of types selected by Ali Baba, and 2. has not been traveled (as a whole) by any of the previous thieves.
   4. If successful, the thief remains waiting in the final chamber reached by his walk. (We assume that each chamber is large enough to accommodate all the thieves that end their walks there.)
3. As soon as a thief is unable to perform his task (each possible sequence of tunnels has already been traversed by someone), the exploration round stops. The last, unsuccessful thief is removed from the cave – Ali Baba uses the thief’s rope to pull him out.

   At this moment, consider the set of chambers that contain at least one thief. The set of chambers will be called significant. (Note that sometimes the significant set may even be empty.)

4. Ali Baba uses the ropes to pull all the thieves out of the cave.

Of course, different choices of the sequence in step 1 can lead to different significant sets of chambers in step 3. Consider the example above. If Ali Baba chooses the sequence ac, he will discover the significant set {2,3}: there will be one thief going 0 → 3 → 2 and two other thieves going 0 → 1 → 3 (each of these two using a different tunnel to get from 1 to 3). The sequence bcb produces the significant set {3}, the empty sequence produces the significant set {0}, and the sequence ccc produces an empty significant set.

Problem specification

You are given the total number n of chambers in the cave. Ali Baba has also told you that they tried to explore the cave using all possible sequences of tunnel types (even though there’s infinitely many of them!) and that they were able to find exactly d different significant sets of chambers.

Find whether such a cave system exists. If yes, find one example.

Input specification

The first line of the input file contains an integer t specifying the number of test cases. Each test case is preceded by a blank line.

Each test case consists of a single line with the two numbers: n and d.

In the easy subproblem E1, 1 ≤ n ≤ 10 and 1 ≤ d ≤ 100.

In the hard subproblem E2, 1 ≤ n ≤ 22 and 1 ≤ d ≤ 10⁹.

Output specification

For each test case, there are two possible outputs.

If there is a cave with the given parameters n and d, output the description of one cave as a sequence of tunnels. In the first line, output the number m ≤ 5000 of tunnels in your cave. (If there is a valid cave, there is always one with much less than 5000 tunnels.) In each of the following m lines, output one tunnel in the form “x y z”, where x is the chamber where the tunnel starts, y is the chamber where it ends, and z is one of a, b, and c. (The chambers in the cave are numbered 0 through n − 1, where chamber 0 is the starting chamber.)

If there is no such cave, output a single line with the integer -1 instead.

You may output additional whitespace. (Note that we do so in the example output for clarity.)

Example

In the first test case the cave we produced has three significant sets of chambers: ∅, {0}, and {1}.

In the second test case our answer is the cave shown on the previous page.

In the third test case it is obvious that there is no such cave.