You wander through a dark dungeon. All around you there are doors of different shapes and colors. You pick one, open it and enter.
“I knew you would come,” said a voice in the dark. You come closer and see an old man with a long white beard sitting on the floor.
“I used to be a problem solver like you,” he says, “but then I took an arrow in the knee.”
“Seriously?” you ask him.
“Well… not really. It’s just what all the kids were saying the last time I saw daylight.”
“So what happened to you?” you ask and sit beside him.
“The truth is, I destroyed my kneecaps on the stairs. When I was younger, I did a lot of programming contests. And in one of them was a really nasty task. I had to determine the number of ways in which one can go up and down a staircase with n steps. Of course, there were some constraints: when going up, you can take two steps at a time, and when going down, you can take up to four steps at once.”
He sighs deeply. “I had no idea how to solve the task, so I found a staircase and attempted to try every possibility. But there were so many of them that I overloaded my knees and now I can’t even walk. So I’m sitting here and still wondering about a solution for that problem. Can you help me to finally put a close on this?”
Problem specification – easy subproblem K1
The staircase consists of n steps. Count the ways of going up and then down the staircase, given the following
constraints:
– On the way up, you can take either 1 or 2 steps at a time.
– On the way down, you can take 1, 2, 3, or 4 steps at a time.
As the actual number of ways can be huge, compute the remainder it gives when divided by 109 + 9.
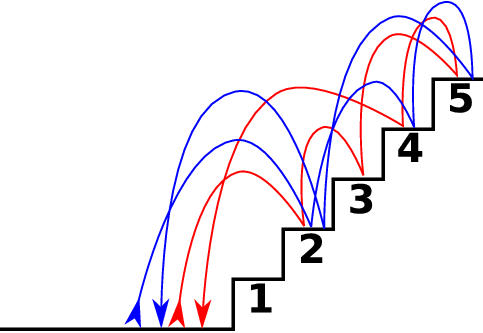
For example, for n = 5 one valid way of going up and down the staircase looks as follows: Start on the ground, ascend to step 2, continue to step 3, and then go to step 5. Having now reached the top of the staircase, you turn around and walk down, first descending to step 4 and then going directly to the ground (which is, at that moment, 4 steps below).
The figure above shows two valid ways of going up and down the stairs for n = 5. The one described above is shown in red.
Problem specification – hard subproblem K2
The staircase consists of n steps. Count all ways of going up and then down the staircase, given the following
constraints:
– On the way up, you can take either 1 or 2 steps at a time.
– On the way down, you can take 1, 2, 3, or 4 steps at a time.
– On the way down, you can only walk on the steps you used on the way up.
Again, your task is to compute the number of valid paths modulo 109 + 9.
In the figure above, the red path is not valid for this subproblem: on the way down we walk on step 4, which was not used on the way up. The blue path (0 → 2 → 4 → 5 → 2 → 0) is valid.
Input specification
The first line of input contains one integer number t specifying number of test cases. Each test case is preceded by a blank line.
Each test case consists of a single line with the integer n (1 ≤ n ≤ 100,000) – the number of steps.
Output specification
For each test case print a single line with one integer – the number of valid paths modulo 109 + 9.
Example
This output is correct for the easy subproblem K1. For example, when n = 3 there are 3 ways to go up, and for each of them there are 4 ways to go back down.
This output is correct for the hard subproblem K2.