Mikey once built a machine that printed the digits of π onto a strip of paper:
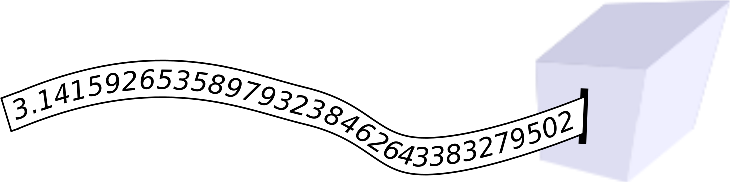
Cut out some segments of the paper strip and assemble them into a valid sudoku square.
People often amuse themselves by looking for some specific sequences of decimal digits in π. For example, Mikey was born on 1992-06-05, so he was pleased to note that the sequence “9265” does indeed appear in π: its first occurrence starts with the fifth decimal digit of π. We say that “9265” occurs at offset 5.
It is often claimed that one can find everything somewhere in π, including the collected works of Shakespeare. However, this is actually still an open problem. Basically, we only know is that the short substrings seem to have a roughly-uniform distribution in the known prefix of π.
Mikey became interested in substrings of π that are permutations of digits 1 through 9. The first such substring is easy to find: “617539284” occurs at offset 2186. The next one follows immediatelly: “175392846” at offset 2187. (Note that these two substrings share 8 of their 9 digits.)
By the time Mikey printed the first 13, 000, 000, 000 digits of π, he already saw each of the 9! possible substrings at least once. (On average, he saw each of them roughly 13 times.) The last permutation of 1-9 to appear was “631279485”. The first offset in π where you can find this particular substring is 12, 944, 969, 369.
A sudoku square is a 9 × 9 square of digits. Each row, each column, and each of the nine highlighted 3 × 3 blocks of a sudoku square must contain each of the digits 1 through 9 exactly once. One valid sudoku square is shown in the following figure.
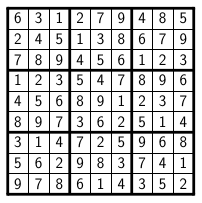
A sample sudoku square
Mikey wants to create a sudoku square using the following process: First, he will take scissors and cut out nine non-overlapping segments of his strip of paper. Each of the nine segments has to contain some 9-digit substring of π that is a permutation of digits 1 through 9. Then, Mikey will place those 9 segments one below another in any order he likes. (That is, each of the pieces of paper becomes one row of a 9 × 9 grid of digits.)
In each subproblem your goal is the same: you have to choose 9 substrings of π and arrange them into rows of a grid in such a way that the resulting grid becomes a valid sudoku square.
In the easy subproblem F1 you can use the first 250, 000, 000 decimal digits of π. Any valid solution will be accepted.
In the hard subproblem F2 you must use a prefix of π that is as short as possible. That is, if we look at the offsets of the substrings you chose, the largest of those 9 offsets must be as small as possible. Any such solution will be accepted.
The output file must contain exactly nine lines. Each line must have the form “string offset”, where “string” is a permutation of 1 through 9 and “offset” is a valid offset into π where this particular string of digits occurs.
The strings must form a valid sudoku square, in the order in which they appear in your output file. The offsets must be small enough (as specified above).
Below is a syntactically correct example of an output file you might submit.
617539284 2186
175392846 2187
631279485 12944969369
123456789 523551502
123456789 523551502
123456789 523551502
123456789 523551502
123456789 523551502
123456789 773349079Note that we would judge this particular submission as incorrect, for two reasons. First, even though all the given offsets are correct, some of them are too large, even for the easy subproblem. Second, that is not a valid sudoku square. (For example, the digit 6 appears twice in the top left 3 × 3 square.)