Internet Problem Solving Contest

• Correct output for K1
• Correct output for K2
• Python program solving both subproblems

Easy subproblem

In the easy subproblem we went through the grid in row major order. Whenever we encountered a bell, we rang it. Just by listening you could determine that there are five rows of bells. If you then just took silent and non-silent segments as zeros and ones, you could easily determine the locations of bells. The grid of bells looks as follows:

 ###     ###    #   #   #####   #####    ###    #   #
#   #   #   #   #   #     #       #     #   #   ##  # 
#       #####   #   #     #       #     #   #   # # # 
#   #   #   #   #   #     #       #     #   #   #  ## 
 ###    #   #    ###      #     #####    ###    #   #

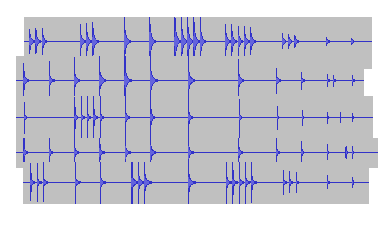
There were many ways how to actually determine the location of bells. For instance, instead of listening to the recording and decoding them manually, you could open the sound file in a sound editor, take a screenshot of the waveform, and then arrange the parts for each bell size below one another. The figure below shows the waveform for the left ear arranged this way. Note that in each row the sounds are getting fainter as we are getting close to the right end of the wall.

Hard subproblem

In this subproblem, each bell rings once and bells ring in random order. So we have to determine the pitch and position of each sound. This is not that hard. The pitch can be found using the Fourier transform and the position can be found by finding the amplitude differences between left and right channel. (Note that you can use the easy input to test your implementation, and as an information source that tells you how the amplitudes change while moving from left to right.)

In our solution we:

1. Split the file into segments of length 0.1 s. Drop segments which are too loud.
2. For each segment determine the mean absolute values of left and right channel. Denote them L and R. We calculate position as P = (L − R)/((L + R)/2).
3. Do the Fourier transform of each segment. Let F be the first frequency which is loud enough.
4. Visualize each segment as a bubble where the x-position is P * abs(P) (for better visualization) and the y-position is F. We also make the size of bubbles proportional to the intensity of the sound.

After that we get following result:

Even with the noise we can see that the answer is JACUZZI. The third letter is indeed C and not O (bubbles on the left edge have three different y-positions but bubbles on the right edge have two).

Bell sounds

The bell samples were created by angstrom and are available online under a Creative Commons 0 license. Thanks!