For any c ≥ 2 the whole table is determined just by 4 of its elements. For example, we can choose the top left 2 × 2 square, which allows us to uniquely compute the first two elements in the bottom row and successively the top, bottom element and from them the middle element of every column. Bruteforcing the top left 2 × 2 square, computing the table using this scheme, and checking whether it fits is enough to solve the easy subproblem.
We can now do the above computation symbolically to notice that there are very strict relationships between the elements of the table. Namely, the middle row must be an arithmetic progression, and the top row (and thus also the bottom row) will always contain two interleaved arithmetic progressions – i.e., cells in odd-numbered columns form one arithmetic progression, the remaining cells form the other one.
Here is one way to derive this result formally. Let’s focus on a 3 × 3 subtable of columns m − 1, m, m + 1. We know that the following five equations must hold:
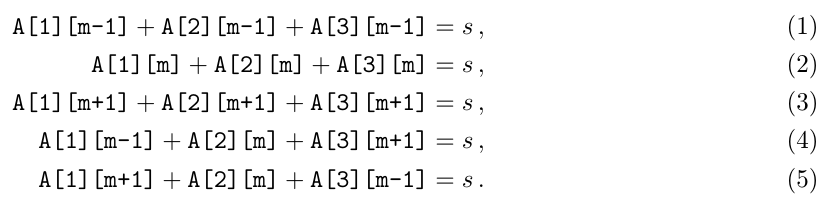
Evaluating (1)+(3)-(4)-(5), we get A[2][m+1] + A[2][m-1] - 2A[2][m] = 0.
In other words, A[2][m+1] − A[2][m] = A[2][m] − A[2][m-1] = d
for any m: the numbers in row 2 must form an arithmetic progression; we denoted its difference by d.
Evaluating the differences (1)-(5) and (3)-(4), we can see that in the top row, there’s one arithmetic progression with difference −d in even columns and another one in odd columns. If we know the top two rows, we can fill row 3 using (due to symmetry, it will contain arithmetic progressions just like row 1). In addition, it’s easy to see that the existence of those three arithmetic progressions automatically satisfies the rule on sums of any three collinear cells. There’s just one remaining condition to satisfy: all numbers must be non-negative.
The minimum elements of an arithmetic sequence are at its ends, so we only need to focus on the end of each of our five sequences. Let’s denote A[1][1] = a, A[2][1] = b, A[1][2] = c. We can make use of symmetry - if we reverse each of a valid table’s rows, d changes sign and the table remains valid. That means we only need to count the case d < 0 twice and add the number of solutions for d = 0, which is the number of triples such that a, b, c ≥ 0; a, c ≤ s − b: ∑(s + 1 − b)2 = (s + 1)(s + 2)(2s + 3)/6.
If d < 0, the sequences in rows 1 and 3 are increasing, so their minimum elements are the first two in rows 1 and 3: a, c, s − a − b, s − c − b − d. The sequence in row 2 is decreasing and its minimum element is b + (c − 1)d. The conditions which need to be satisfied are
For a fixed b and d, the number of pairs a, c is (s − b + 1)(s − b + |d|+1). Their sum over all allowed b for a fixed d < 0 is an ugly polynomial in s, |d| and its sum over all allowed d (that is, for |d|≤⌊s/(c−1)⌋) is an even uglier polynomial in s only (to be precise, only if we limit ourselves to a fixed value of $s\bmod (c-1)$, since only that gives a linear dependence of ⌊s/(c−1)⌋ on s); the same holds for the final answer. Since each summation increases the degree of the polynomial by 1, the resulting polynomial will have degree 4.
Rather than computing it by hand or even through Wolfram Alpha, it’s easier to compute answers for several small values of s (it’s sufficient to take $s\bmod (c-1)+k(c-1)$ for 0 ≤ k ≤ 4) by trying all b, d and summing up the number of choices for a, c; using these values of a polynomial in points (yk, xk = k), we can interpolate the answer as
where division by k − j can be handled with precomputed modular inverses. Time complexity: O(c2).
You can try finding the polynomial in x from the decomposition s = x(c − 1)+r, e.g. using WolframAlpha. It allows us to compute the answer in O(1) and it only has 25 terms!