One day a group of friends jumped into their 2n cars and they all went for a road trip into the lake district. The cars were numbered 1 through 2n. Initially, they were driving in this order.
During the road trip the convoy encountered multiple ferries, one after another. Each ferry in the district was exactly large enough to accommodate the 2n cars, and there were no other cars around at any time. Whenever the cars used a ferry, their order got mixed up. This is due to the way the ferries are loaded and unloaded.
A ferry is a long and narrow boat. There is just enough room for two columns of cars, each containing n cars. When loading the ferry, the first n cars form the first column and the last n cars form the second column. When unloading the ferry, all cars are allowed to drive away at the same time, so they have to zip in order to form a single convoy. The first car in the new order will always be the first car from the right column, the second car will be the first car from the left column, the third car will be the second car from the right column, and so on, alternating right and left.
There are two types of ferries. On type-L ferries the crew instructs the cars to fill the Left column first while on type-R ferries cars fill the Right column first. Note that the ferry type does not influence how the cars leave the ferry. The first car to leave is always the first car in the right column.
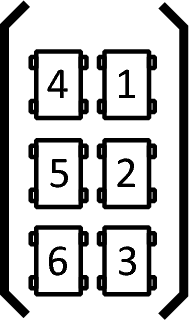
Above: Cars 1 through 6, in this order, just boarded a type-R ferry (from the bottom of the figure). The cars will leave this ferry in the following order: 1, 4, 2, 5, 3, 6.
The trip is now over. Your car was car x, which means that at the beginning your car was the x-th car from the beginning. You remember a sequence a1, …, ak of positive integers. The number ai means that at some point in time your car was the ai-th car from the beginning of the convoy. The numbers in your sequence are in chronological order: your car was ai-th before it was ai + 1-th, for all i.
Compute the smallest possible number f of ferries you encountered during the trip. Produce a proof: one possible sequence of exactly f Ls and Rs such that it is possible that the f ferries you encountered were type-L and type-R ferries in the given order.
The first line of the input file contains an integer t = 100 specifying the number of test cases. Each test case is preceded by a blank line.
Each test case consists of two lines. The first line contains the integers n, x, and k, where 1 ≤ x ≤ 2n. The second line contains the integers a1, …, ak.
In the easy subproblem F1, 1 ≤ n ≤ 105 and 1 ≤ k ≤ 20.
In the hard subproblem F2, 1 ≤ n ≤ 1018 and 1 ≤ k ≤ 104.
For each test case, output a single line with the number f, a colon, and one possible shortest string of Ls and Rs. Note that there are no spaces in the output.
Input:
3
10 1 3
1 1 1
10 1 2
2 4
3 2 4
5 3 1 2Output:
0:
2:LL
7:RRLRRLLIn the first example there were no ferries, the car simply remained in the first place.
In the second example the first type-L ferry moves the car to position 2 and the second such ferry moves it to position 4.
In the third example RR gets us from 2 to 5, L from 5 to 3, RRL from 3 to 1, and L from 1 to 2.