The easy subproblem can be solved by finding a single valid solution and then padding it with an appropriate number of mines. Each instance that satisfies the constraints for the easy subproblem is solvable.
Below, we give a solution to the hard subproblem. We aim to present a solution that reduces the need for a manual case analysis to a minimum.
Theorem 1. In any valid solution the revealed zeros must form a full rectangle.
Proof: All revealed zeros form a connected component. Imagine walking around the outer boundary of this component (along the grid lines between cells) in counter-clockwise direction. If we only take left turns, the outer boundary must be a rectangle. If we ever take a right turn, we must have the situation shown in the figure below. However, this cannot happen in a valid solution: the revealed non-zero cell B must contain a 1, and thus the player can now determine that the hidden cell A must contain a mine.
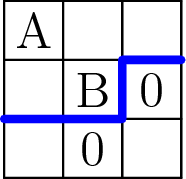
Above: a right turn on the ccw boundary of a component of zeros. The thick line shows one possible continuation of this boundary. Cell B must be a 1, and cell A must be a mine.
Thus, the only possibility is that the outer boundary of the component of zeros is a rectangle. Furthermore, there can be no non-zero cells in this rectangle, otherwise we could take the non-zero cell with the lexicographically smallest coordinates and we would have exactly the same situation that was shown in the figure above.
In the next step of our solution we will solve the special cases with r ≤ 2 or c ≤ 2. These cases are discussed in detail at the end of this solution, for now we’ll skip them and we’ll focus on the big picture instead. Without loss of generality, we now may assume that 3 ≤ r ≤ c.
Theorem 2. If r, c ≥ 3, a valid solution cannot contain a revealed 0 that is exactly one cell away from the border of the board.
Proof: Suppose we have the situation shown in the first figure below: a revealed cell with a 0 that is one cell away from the border, and a revealed cell A that contains a positive number. A situation like this one cannot occur in a valid solution.
Why is that? The cell above the 0 must obviously contain a 0 as well. The cell above cell A cannot be a 0, otherwise we would have the situation shown above once again. It cannot be a 2, because then the cell to the right of it would have to contain a mine. Thus, we must have the situation shown in the second figure below.
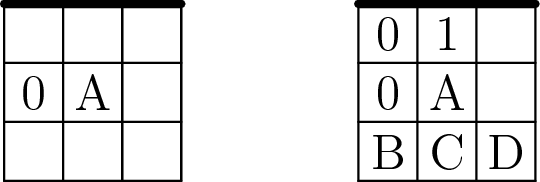
Above: the deduction from seeing a zero and a nonzero one cell away from the border. (The thick line denotes the border of the game board.)
However, this last possibility will also lead us to a contradiction. We know that cell B cannot contain a mine, hence A is either 1 or 2. If A = 1, the player will be able to conclude that cell D is empty. And if A = 2, the player will be able to deduce that cell D must contain a mine. In either case, our evil plan fails.
Thus, whenever we see a revealed 0 in the second row of the grid, the only remaining possibility is that the entire second row are 0s. However, this then produces a 0 in the second column. By repeating the same argument, the second column must be all 0s as well. From Theorem 1 we know that revealed zeros form a rectangle – but given what we know, the only possibility is that the entire board is a rectangle of zeros, and that cannot happen.
This concludes our proof: a revealed 0 in a cell that is one cell away from the border can never appear in a solution.
Theorem 3. If r, c ≥ 3, there is no valid solution if the player clicks a corner cell.
Proof. Let’s label the cells as shown in the figure below. From Theorem 2 we know that A, B, and C must all contain positive numbers.
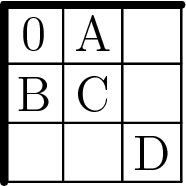
Cells A and B must both be 1s, otherwise the player would be able to determine the contents of their hidden neighbors. Then, C must be either 2 or 3. If C = 2, the player can be sure that D is empty, and if C = 3, the player can be sure that D contains a mine. Thus, there is no valid solution in which we reveal the corner.
At this moment we know that there are only two types of valid solutions left:
The revealed zeros all lie along a single border of the board (without coming too close to either corner).
The revealed zeros form a rectangle somewhere inside the board, at least two cells away from each border.
There are valid solutions of both these types. How can we analyze them? By using a simple brute force approach. Suppose we fix the rectangle of revealed zeros. We know that the cells at distance 1 from the rectangle are precisely all the revealed cells with positive integers. We can now do the following:
Construct the set of cells that are in distance 2 from the rectangle.
Try all possible placements of mines onto these cells.
For each placement of mines compute the numbers revealed in the cells around the rectangle of zeros.
Divide the placements of mines into “equivalence classes” according to the revealed numbers.
For each possible sequence of revealed numbers, look at all placements of mines in that “equivalence class” and check whether they have the desired property. (I.e., whether each cell at distance 2 from the revealed zeros can, but does not have to contain a mine.)
Clicking a cell at the border, smallest number of mines.
Suppose that r ≥ 3 and c ≥ 6. (Smaller cases can be solved by examining all possibilities.)
If the player clicks a cell at the border, we will need at least 4 mines. If m < 4, there is no solution. Why? If we reveal a single zero, the best we can do is shown in the figure below.
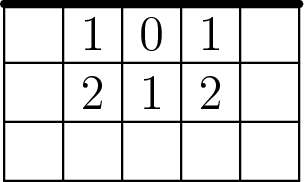
The cells at distance 2 from the zero contain either 3 or 4 mines, and each of those cells can, but does not have to contain a mine. If we now have an arbitrarily large board, we can place three mines at distance 2 from the zero, and the fourth mine anywhere we like. This shows that 4 mines are sufficient.
We can easily show that 4 mines are also necessary. We know (by trying all possibilities) that we cannot use fewer if we only reveal a single zero. If we reveal at least two zeros, we’ll have a situation like the one shown below.
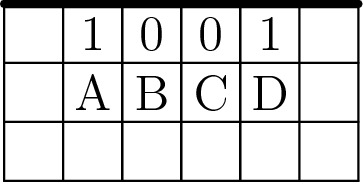
There are at least two mines – each adjacent to one of the 1s. The values A and D cannot be 1s, so there are at least two other mines, each adjacent to one of those numbers.
Clicking a cell at the border, largest number of mines.
Again, we’ll start by looking at what happens if we just reveal a single zero. The best we can do now (i.e., the most mines) is the configuration shown below. There are either 5 or 6 mines at distance two from the 0.
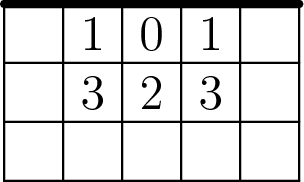
In other words, among the cells that are at distance at most two from the 0, there are 9 or 10 cells that are not mines. Thus, if we reveal this pattern to the player, we can produce valid solutions with up to rc − 10 mines.
Can we do better than that? Clearly we cannot. If we reveal more than one zero, we can easily show that there will always be at least 10 cells that don’t contain a mine.
Thus, we have shown the following results for the click on a border:
We cannot have fewer than 4 mines.
If we use the first pattern, we can create solutions with 4…rc − 12 mines.
If we use the second pattern, we can create solutions with 6…rc − 10 mines.
We cannot have more than rc − 10 mines.
And as for r ≥ 3 and c ≥ 6 those two ranges overlap, we are done – all the counts of mines from 4 to rc − 10 are possible.
Clicking a cell inside the board.
Suppose that r ≥ 5 and c ≥ 6. (Smaller cases can be solved by examining all possibilities.)
Now we are going to do the same thing again, but this time for a clicked cell that is at least 2 cells from each border. We’ll skip the details and we’ll just show the patterns. (We constructed them by brute force, just to be sure we didn’t miss anything, but it’s perfectly feasible to construct them by hand as well – as soon as you realize that you just want a 3 × 3 square.)
The pattern for the fewest mines is shown on the left. There are either 4 or 5 mines at distance two from the 0. The pattern for the most mines is shown on the right. The cells at distance two contain either 11 or 12 mines – in other words, there are either 13 or 14 non-mine cells at distance at most two from the click. As before, it is very easy to show that we cannot have fewer/more mines if we reveal more than one 0.
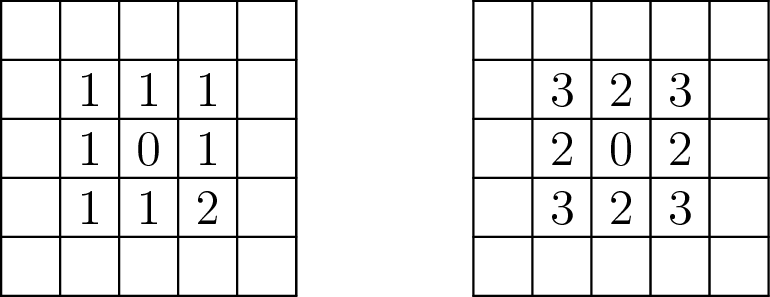
Hence, the conclusion for clicking inside a large board is that we can have between 5 and rc − 14 mines, inclusive. All that remains are the special cases we skipped before: the very narrow boards.
Boards of height 1.
So simple: there is never a solution. The first non-zero digit you’ll reveal must be a 1, and the player will know that the next cell has a mine.
Boards of height 2.
Most of this was spoiled in the example in the problem statement. The clicked cell will be a 0. The cell above/below that cell will also be a 0. Thus there are only two possible types of revealed cells, as shown below.
0001.. ..1001..
0001.. ..1001..For each of these we can easily find the smallest and largest number of mines we can use.