Internet Problem Solving Contest

• Easy input data set – E1
• Hard input data set – E2 (generator)

You’re a rich tycoon who owns an enormous transportation company. Your current project is a new railroad that will go across the whole country and bring you grossly huge gross profit. But before you can start building the railroad itself, there are terrain adjustments to be made.

On a satellite image (i.e., looking from above), the future location of the railway appears as an infinite straight line. But you’re more interested in the terrain’s elevation profile (i.e., looking at the side view). Right now, everything is completely flat. That’s boring! You need some more interesting scenery so that tourists will pay you lots of money. Since you’re so rich, you decided to make some hills and valleys.

Problem specification

You took the satellite image and made a mark every 1 meter. You assigned those marked points coordinates from negative infinity to positive infinity.

The elevation (terrain height) at every point is an integer amount of meters. Between them, the ground is always a straight slope connecting the nearest two points. Your engineering department has informed you that train engines can’t handle very steep slopes, so the difference in elevation between two neighboring points can be at most 1 meter.

For example, part of an elevation profile that is suitable for trains could look like this:

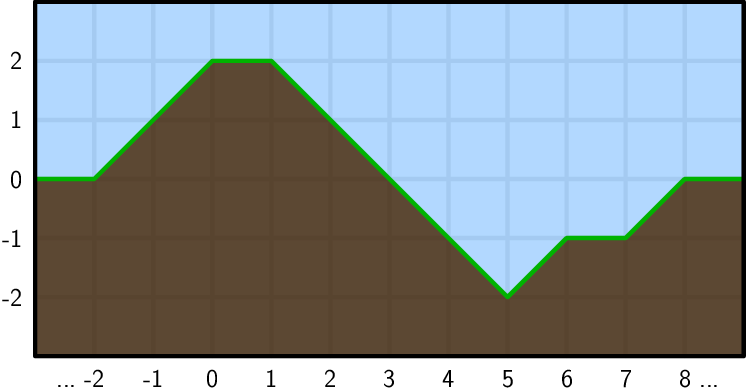
Each change to the terrain must also leave it suitable for trains. This means that whenever raising a point would cause it to be too far away from its neighbor, you must also raise that neighbor. Lowering a point works the same. For example, if you want to raise point 3 by one meter, you must also raise points 4 and 5 as shown below:

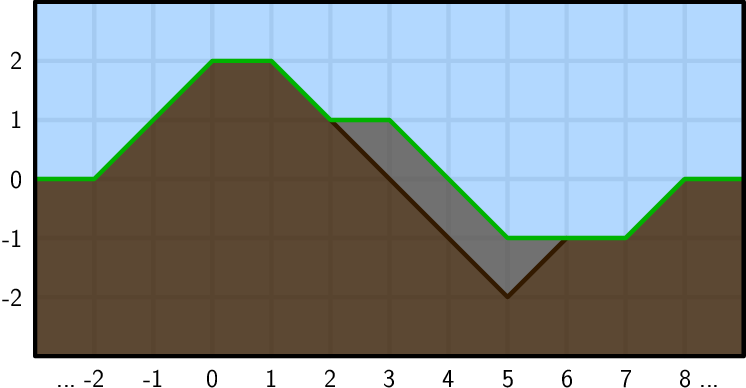
The cost of raising or lowering terrain is equal to the number of square meters of dirt you added or removed. In our example, to raise point 3 you had to add 3 square meters of dirt.

Initially, all points have the same elevation. You have given your construction workers a list of commands to increase or decrease the elevation of various points by 1 meter. The workers will complete the commands in the given order, one at a time (each time also raising or lowering other points if necessary). Now you’d like to know the cost of each command.

Input specification

The first line of the input file contains an integer t specifying the number of test cases. Each test case is preceded by a blank line.

The first line of each test case contains the number of commands n. The i-th of the following n lines contains two integers p_i and e_i describing the i-th command: the coordinate of the point to be changed, and whether to raise it by 1 meter (e_i = 1) or lower it by 1 meter (e_i = −1).

In the easy subproblem E1, 1 ≤ n ≤ 1 000 and −1 000 ≤ p_i ≤ 1 000.

In the hard subproblem E2, 1 ≤ n ≤ 5 000 000 and −10⁹ ≤ p_i ≤ 10⁹.

Because e2.in is about 60 MB, you cannot download it directly. Instead, we have provided a small Python 2 program e2gen.py that will generate e2.in when executed. The generator should take under 1 minute to run on average hardware. We recommend running it early – for example, starting it as you start working on your solution for this problem.

Output specification

For each test case: Let c_i be the cost of command i, for all 1 ≤ i ≤ n. (Note that all c_i are positive integers.) Then, let d_i = i ⋅ c_i. Output one line with a single number: $(d_1 + \cdots + d_n) \bmod (10^9 + 9)$.

Example

Input:

1

8
0 1
5 -1
1 1
5 -1
1 1
0 1
7 -1
3 1

Output:

71

The costs are 1, 1, 1, 3, 2, 2, 1, 3. The last command corresponds to the change from the first to the second picture in the problem statement.