“Draw seven red lines, all of them strictly perpendicular to each other, some of them with green ink and some of them with transparent ink. Also, one of them should be in the form of a kitten.”
(The Expert)
Oh, don’t worry, your task is much simpler. We’ll stay in the two-dimensional plane.
A straight line cuts the two-dimensional plane into two regions. With two such lines you can cut the plane either into three regions (if you use two parallel lines) or into four regions (if you use lines that intersect each other).
Below are some ways of arranging three lines to cut the plane into 7, 6, and 6 regions, respectively.
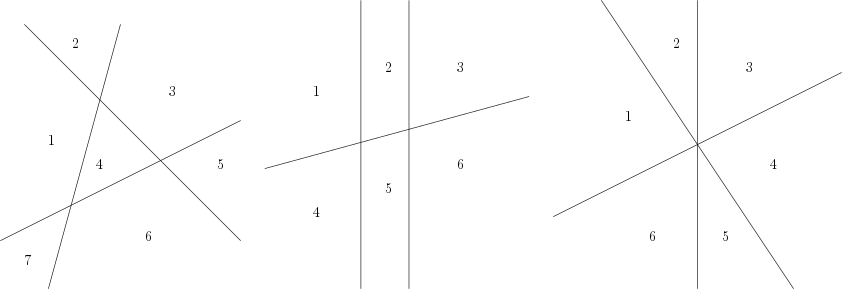
We want to divide the plane into r regions. Tell us how to draw the lines.
In the easy subproblem J1 you may output any set of lines that divides the plane into exactly r regions and satisfies the output format described below.
In the hard subproblem J2 you must also divide the plane into exactly r regions, but this time you must use as few lines as possible.
The first line of the input file contains an integer t ≤ 1000 specifying the number of test cases. Each test case is preceded by a blank line.
Each test case is a single line with a single integer 1 ≤ n ≤ 1000: the desired amount of regions.
The output for each test case should start with a line with a single integer ℓ: the number of lines you want to draw. Then, output ℓ lines, each describing one line in the plane. Each line is specified by two space-separated integers m and b. These represent the line with the equation y = mx + b. (You are not allowed to draw vertical lines. Obviously, you don’t need to do so.)
For every test case you can use at most 1 000 lines. All slopes (m) and y-intercepts (b) have to be between −10 000 and 10 000, inclusive. It is guaranteed that such solutions exist for all valid test cases.
Input:
3
2
4
35Output:
1
0 5
2
2 0
-2 4
10
2 0
1 1
0 1
0 2
0 3
0 4
0 5
0 6
-1 3
-2 4In the first sample, there is just one line, and that always divides plane into 2 regions. In the second sample, two intersecting lines divide plane into four quadrants. The solution shown for the third case is not optimal, and hence it would not be accepted in the hard subproblem.