The input file contains a coordinate grid with 10 × 10 similar-looking shapes. Among those 100 shapes there are exactly three matching pairs of shapes:
Two shapes are identical. (One can be obtained from the other by rotation and translation only.)
Two shapes are mirror images of each other. (They are not identical as defined above, but one can be obtained from the other by flipping it once and then rotation and/or translation.)
Two shapes are complements of each other. (Explained below.)
As you can see from the input file, the shapes are actually pictures of simple graphs on 7 vertices. “Complements” should be interpreted in that sense. Two shapes are complements of each other if one of them can be rotated and translated – without flipping – and placed on top of the other in such a way that their vertices coincide and each pair of vertices is connected by an edge in exactly one of the two graphs.
In order to solve the easy subproblem M1, find any one of the three matching pairs.
In order to solve the hard subproblem M2, find all three matching pairs.
The input is a PNG picture of the shapes. The input is the same for both subproblems.
For the easy subproblem M1 output one line with two space-separated tokens: the coordinates of two shapes that form any one of the three matching pairs. Coordinates of a shape should be printed in the form “LN”, where L is a letter and N is a number.
For the hard subproblem M2 output three lines, each containing two space-separated tokens: the coordinates of the two shapes that form one of the three matching pairs. Output each matching pair exactly once.
The order of the two shapes within a matching pair does not matter. The order of lines in the output for M2 also does not matter.
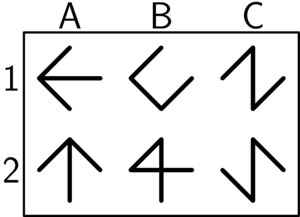
The example input shown above contains six graphs on four vertices. The three matching pairs are the following ones:
The identical shapes are A1 and A2. You can rotate A1 by 90 degrees to the left to get A2.
The mirror images are C1 and C2. They are not identical but C2 is a vertical mirror image of C1.
The complementary shapes are B1 and B2. You can rotate B2 by 90 degrees to the right and place it on top of B1 to get a complete graph – a square with both diagonals. Note that each of the six edges of the complete graph is present in exactly one of the shapes B1 and B2.
One possible output for the easy subproblem:
C2 C1One possible output for the hard subproblem:
A1 A2
B1 B2
C1 C2The same problem but with fewer (49 instead of 100) different shapes was used in one of the rounds of the 2016 World Puzzle Championship. However, this is IPSC and bigger is always better, right? :)