Internet Problem Solving Contest

• Easy input data set – K1
• Hard input data set – K2

Kelly is drawing pictures with circles. In order to draw a picture, she does the following:

1. She draws a horizontal line segment of length 1 and she assigns the coordinates 0 and 1 to its left and right end, respectively.
2. She draws two equally big circles that touch the line of the segment from above (one at each end of the segment) and touch each other above the middle of the segment. These two circles become her active circles.
3. She draws a third circle that touches the line segment and both active circles.
4. She chooses a sequence of n ≥ 0 directions, each being either “left” or “right”.
5. Exactly n times she repeats the following:
   1. She looks at the next direction. Only one of the two active circles remains active: the one that touches the segment farther in that direction.
   2. The most recently drawn circle becomes active.
   3. She draws a new circle that touches the segment and both active circles.

For example, this is the picture she would draw for the sequence “left, right, left”. Circles were drawn in the order red, orange, green, blue. (The blue one is quite tiny, don’t miss it!)

As boys often do, Kevin forgot his compass at home. But he also likes pretty pictures, so he decided that he will do the same with squares (rotated 45 degrees, so that their diagonals are parallel to the coordinate axes). For example, for the sequence “left, right, left” Kevin would draw this:

Problem specification

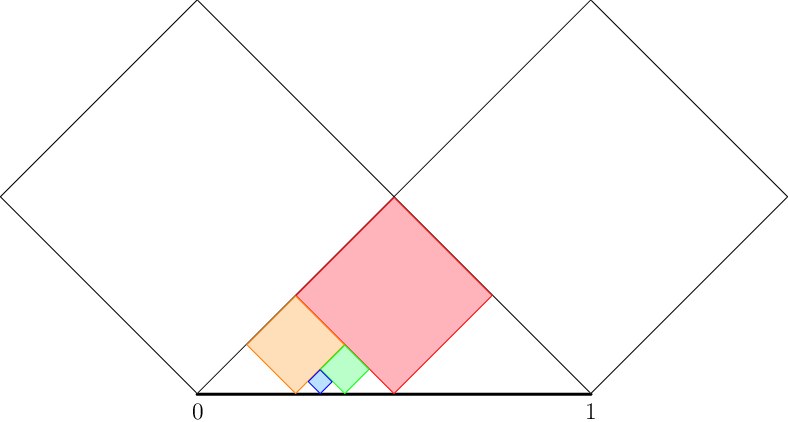
The “circles-to-squares” function c is defined as the only continuous function on [0, 1] with the following property: For any sequence of directions, if Kelly drew her picture and the last circle touches the segment at x_c, and Kevin drew his picture and the last square touches the segment at x_s, then let c(x_c)=x_s.

You will be given a collection of inputs for c. Compute the corresponding outputs.

Input specification

The first line of the input file contains an integer t ≤ 100 specifying the number of test cases. Each test case is preceded by a blank line and consists of a single line.

Each test specifies the number x_c for which you must compute c(x_c). Decimal numbers are not exact, so the inputs are specified as roots of polynomials. Each test case has the form “p k”, where p is a polynomial with integer coefficients (see below) and k is a positive integer. Find the k-th smallest distinct real root of p and use that value as x_c. It is guaranteed that it exists and lies in [0, 1].

In the easy subproblem K1 each p is linear. (Therefore, every x_c is a rational number.)

In the hard subproblem K2 each p is either linear or quadratic.

Additionally, the input will be such that each line of correct output will have fewer than 40,000 characters.

Output specification

For each test case, output a single line. If the corresponding x_s = c(x_c) is an algebraic number (i.e., it can be expressed as a root of a polynomial with integer coefficients), output it using the same formatting as in the input. You must output the polynomial with the smallest possible positive degree. If the corresponding x_s is transcendental, output the line “transcendental” instead.

Polynomial formatting for input and output

• The description of a polynomial does not contain any spaces.
• The powers of x in a polynomial are printed in descending order.
• Every term is written as a*x^n where a and n are integers, except that a*x^1 is written as just a*x, and a*x^0 as just a.
• All powers of x are explicitly mentioned, even if their coefficient is zero. (E.g., 2*x^2+3 is invalid.)
• The leading term has a positive coefficient. (E.g., 0*x^2+1*x+1 and -1*x+2 are invalid.)
• All coefficients are always explicitly mentioned, even if they are 0 or ±1. (E.g., x^3-x^2+x+1 is invalid.)
• There is no d > 1 that divides all coefficients of the polynomial. (E.g., 2*x+2 is invalid.)

Examples of correctly formatted polynomials include “1*x^3+0*x^2+0*x-0” and “7*x^2-47*x+123456”. For more examples see the input files directly.

Example

Input:

2

2*x-1 1

3*x-1 1

Output:

2*x-1 1
4*x-1 1